Skip to main content

The Internals of SHA 256 Algorithm

 I came across this excellent video, explaining how the SHA-256 algorithm works internally. I had always been excited to understand how a real-world hashing algorithm works internally. SHA-256 is one of the most popular hashing algorithms, so after getting my hands on that video, I knew I had to try and implement this on my own. This feels like once in a lifetime opportunity. So here I am after having implemented the algorithm on my own and feeling confident understanding how SHA-256 works. I want to pass on that same confidence to the readers of this blog (probably including me in a few months :D) along with code snippets. So, lets dive right into it...

Basic Operations

There are some basic operations that the SHA-256 algorithm builds on top of. Here is a list of those:

1. Shift Right - Shifts the bits of the original number pos bits to the right, dropping of things that slide of the end.

2. Rotate Right - Rotates pos bits in the original number. Very similar to shift but instead of dropping things off the end, it wraps them at the beginning (in a circular fashion)

3. σ0 (lowerSigma0) - Combination of rotations and shifts defined above.

4. σ1 (lowerSigma1) - Another combination of rotation and shifts.

5. Σ0 (upperSigma0) - Combination of rotations.

6. Σ1 (upperSigma1) - Another combination of rotations.

7. Choice - Given three binary numbers x, y, z, depending on the bits of x, choses the corresponding bit in y if x bit is 1, or the corresponding bit in z if x bit is 0.

8. Majority - The result contains the majority bit out of each bit of x, y and z.

The SHA-256 Algorithm


The above picture shows the various steps of the SHA-256 algorithm. This is the SHA256 algorithm in code that I implemented:


Here is each of the steps broken down:

1. Convert the original message (usually string) in the binary format. (If the string is "abc", it gets converted to 011000010110001001100011, where first 8 bits are "a" (96 ASCII), next 8 are "b" (97 ASCII) and next 8 are "c" (98 ASCII).


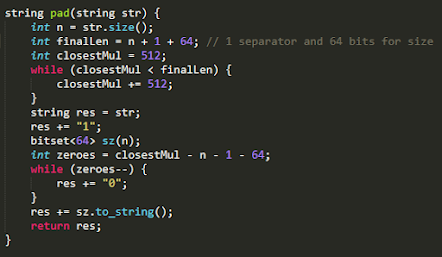
2. Pad the binary message in such a way that the total number of bits in the padded message are a multiple of 512. Also, 65 bits of the padded message are reserved. A bit "1" is added right after the original message as a separator. Then there are a bunch of zeroes, and the last 64 bits encode the length of the original message.


3. Now that the message length is a multiple of 512, we just break it into message blocks which are 512 bits in length each.


4. Next step is to process each message block one by one and create a message schedule out of each block eventually compressing each of the message schedule.


5. In order to create a message schedule, we break down the 512 bit message block into 16 words of 32 bits each. However, a message schedule consists of 64 words. This is where the basic operations we defined above come into play. We use some combination of those to generate the remaining 48 words. At the end of all of this, we have transformed a 512-bit message block into 64, 32 bits word message schedule.


6. Now comes the heart of the SHA-256 algorithm, the compression stage. Now that we have 64 words of 32 bits size with us, we need to merge them in some way. SHA-256 does that by merging them down to 8, 32-bit hash values. These hash values are initialized as below:


They might look intimidating (anything in hexadecimal looks intimidating to me :D) but these are just the square roots of the first 8 primes. (Their fractional part, to be precise)

And these hash values, are the ones that store the final result after processing each message block. As shown in the block diagram above, the updated hash values after each step are used as an input in the next step. The square root of first 8 primes is the initial hash value with which all this process starts.


7. This process of creating a message schedule and compressing it is repeated for each message block. And the final hash values, generated after processing the last message block gives us the SHA-256 hash. We convert each hash value into the 8-length hexadecimal equivalent and concatenate all of them to generate the 64-length SHA-256 hash. 



And that is how the SHA-256 algorithm works. Here is the full C++ source code for the algorithm:


I hope, this post gives you confidence around the SHA-256 algorithm and maybe even the motivation to implement it yourself (probably improving over my quick and kind of dirty implementation) in the programming language of your choice.

Comments

Post a Comment

Popular posts from this blog

Streaming Algorithms - Lossy Counting

We had a discussion recently in our office on one of the famous  streaming algorithms  known as lossy count. I decided to write down my understanding of it focusing on the space complexity discussion and proving why it works in logarithmic space. This  is the original paper introducing this algorithm and most of the information discussed in this blog is (hopefully) a simplified version of this paper relating to lossy count. Problem Statement There are use cases where you may be receiving a continuous stream of data and you want to know which items in that data stream exceed a certain threshold. The data stream could be really big so you can't store it in memory. Moreover you want to answer queries in real time. So here are the challenges this problem imposes: 1. Need to do it in single pass (time constraint) 2. Limited memory 3. Large volume of data in real-time The above issues warrant the need of a smart counting algorithm. Data stream mining to identify events & patterns can
Post a Comment
Read more

RSA Encryption System

THE NEED OF ENCRYPTION In today's world where a lot of secured information like our credit card number, passwords etc., travel around the web, the presence of a secure encryption system is almost inevitable. We want a method to encrypt a message, send it over the insecure internet connection and allow only the receiver to be able to decrypt and read the original message. This exact problem was solved by R ivest, S hamir and A dleman(RSA) in the year 1978, in their paper A Method for Obtaining Digital Signatures and Public-Key Cryptosystems. In this post, I will try to explain the method they adopted to create a secure encryption system. PUBLIC KEY CRYPTOSYSTEM A public key cryptosystem has the following properties: 1) D(E(M)) = M, if we decrypt an encrypted message, we should get back the message. 2) Both E and D should be easy to compute, if it takes days to encrypt or decrypt the message, then the cryptosystem is not very useful. 3) By publicly revea
1 comment
Read more

Consistent Hashing

 I have been meaning to write this blog for some time now but somehow kept on postponing (read procrastinating...). I read about this technique of Consistent Hashing a while back and was mesmerized by its elegance. Recently read it again in this brilliant blog and thought of expressing it in my own words for posterity. So let us begin. Hashing I won't talk too much about hashing since it is a very basic computer science concept. In a word, it means mapping an object to another object. Or more generally, mapping a key to a value where their types don't matter. Mostly the mapping is from a string to int.  There could be multiple different hash functions that can exist which randomize the how the keys are hashed to the values. We are going to consider a simple use case where let's say you have N different servers and there are multiple keys that you want to distribute among those servers. How do you do it? Well, a simple strategy is that you have a function which applies some
Post a Comment
Read more